关于位运算的新发现（2021年06月22日）

发现历程

2021年06月21日晚上，在做算法题的时候遇到了二进制的位运算相关内容，位运算包括与运算、或运算、异或运算、取反等等。

我感觉平时在编程的时候更多的是主要用加减乘除以及求余数运算，在位运算这方面比较欠缺和薄弱，于是我打算先探索一下二进制位运算中的与运算的规律。

与运算方法

6 & 2 = 2

6 的二进制表示是 110， 2的二进制表示是 10

所以按位与运算就是
1
2
3
4
110
010
---
010
每一个位相互比较，如果都是1，那么这一位的结果就是1，其他情况就是 0

结果是 010，就是2

我打算把所有数字与所有数字的与运算写出来，就像九九乘法表一样，做成一个16x16的表格，看看有没有规律

手写表格

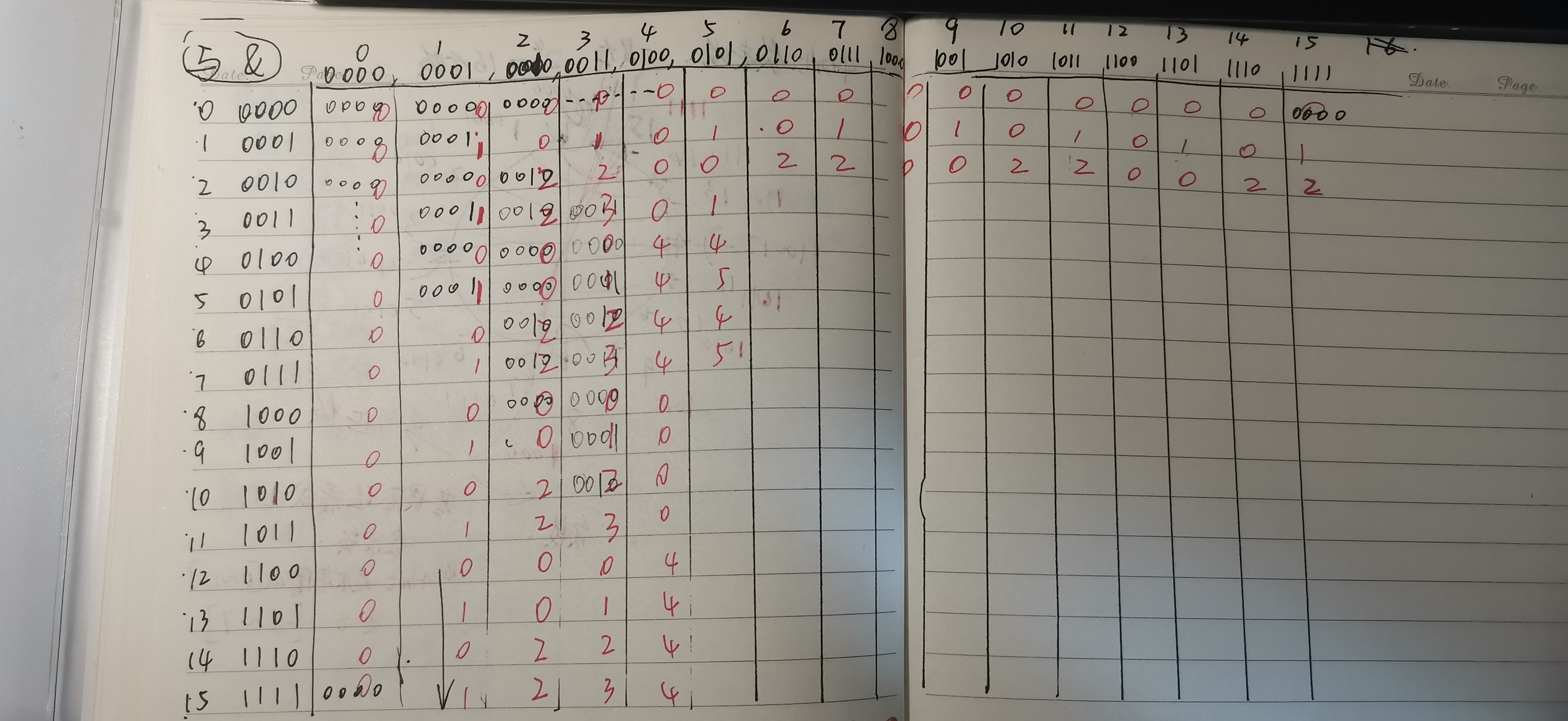
（由于是草稿，写的字比较潦草）

好像是有一点规律，但是表格太大了，看着也不够整齐，于是我想用编程的方式直接输出，这样更加方便

for i in range(16):
    for j in range(16):
        n = i & j
        print(n, end="/t")
    print()

输出结果

0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	
0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	
0	0	2	2	0	0	2	2	0	0	2	2	0	0	2	2	
0	1	2	3	0	1	2	3	0	1	2	3	0	1	2	3	
0	0	0	0	4	4	4	4	0	0	0	0	4	4	4	4	
0	1	0	1	4	5	4	5	0	1	0	1	4	5	4	5	
0	0	2	2	4	4	6	6	0	0	2	2	4	4	6	6	
0	1	2	3	4	5	6	7	0	1	2	3	4	5	6	7	
0	0	0	0	0	0	0	0	8	8	8	8	8	8	8	8	
0	1	0	1	0	1	0	1	8	9	8	9	8	9	8	9	
0	0	2	2	0	0	2	2	8	8	10	10	8	8	10	10	
0	1	2	3	0	1	2	3	8	9	10	11	8	9	10	11	
0	0	0	0	4	4	4	4	8	8	8	8	12	12	12	12	
0	1	0	1	4	5	4	5	8	9	8	9	12	13	12	13	
0	0	2	2	4	4	6	6	8	8	10	10	12	12	14	14	
0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15

右下角的两位数部分好像有一点奇怪的形状，

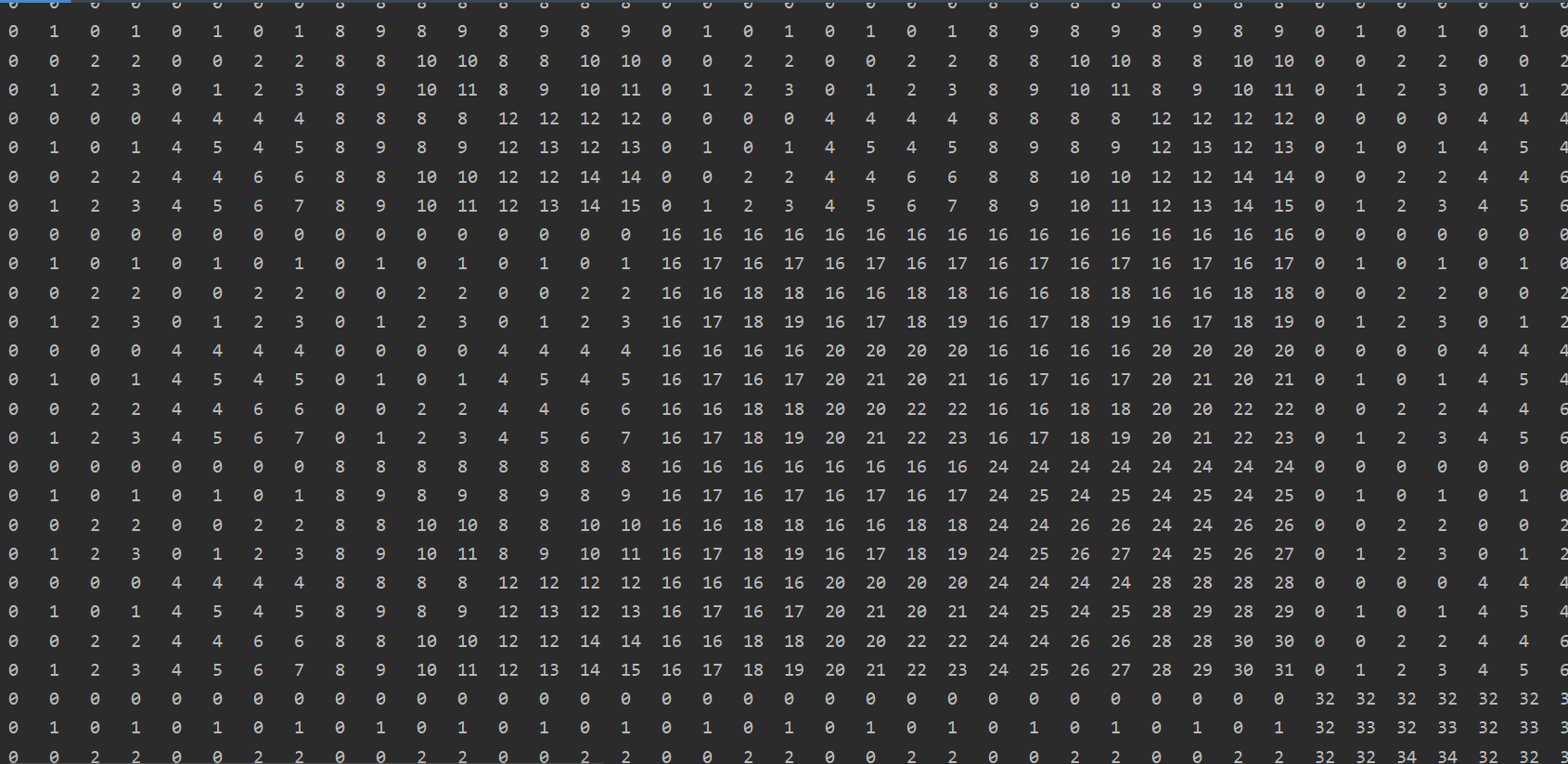
于是我继续扩大范围，发现了这所有二位数的部分似乎组成了一个奇妙的形状！这让我想起了分形结构。

于是我觉得应该还可以再直观可视化一些，于是我就让程序输出成一张图片，我们都知道图片通常是有像素点矩阵组成的像素点，矩阵里的数字可以用像素点的亮度，也就是灰度来表示，这样就更加直观了。

于是我改了一下代码，由于像素点太小了，我顺便也扩大了表格的边界到256

N = 256
im = Image.new('RGBA', (N, N), (0, 0, 0))
for i in range(N):
    for j in range(N):
        n = i & j
        im.putpixel((i, j), (n, n, n))
im.show()